Nonlinear PCA

Nonlinear PCA toolbox for MATLAB

by Matthias Scholz 		Nonlinear PCA (NLPCA) - Autoencoder neural network
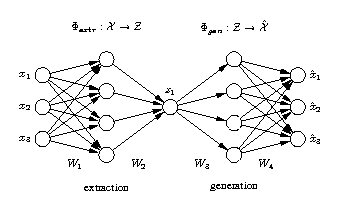
Auto-associative neural network (Autoencoder)

Nonlinear principal component analysis (NLPCA) is commonly seen as a nonlinear generalization of standard principal component analysis (PCA). It generalizes the principal components from straight lines to curves (nonlinear). Thus, the subspace in the original data space which is described by all nonlinear components is also curved.
Nonlinear PCA can be achieved by using a neural network with an autoassociative architecture also known as autoencoder, replicator network, bottleneck or sandglass type network. Such autoassociative neural network is a multi-layer perceptron that performs an identity mapping, meaning that the output of the network is required to be identical to the input. However, in the middle of the network is a layer that works as a bottleneck in which a reduction of the dimension of the data is enforced. This bottleneck-layer provides the desired component values (scores).

linear PCA

PCA 		The left plot shows standard PCA applied to a simple two-dimensional data set. The two resulting components are plotted as a grid which illustrates the linear PCA transformation. The plot on the right shows nonlinear PCA (autoencoder neural network) applied to a 3/4 circle with noise. Again, the two components are plotted as a grid, but the components are curved which illustrates the nonlinear transformation of NLPCA.

nonlinear PCA

NLPCA - Nonlinear PCA - Autoencoder neural network
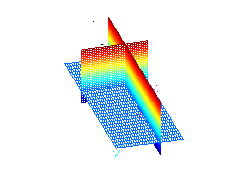
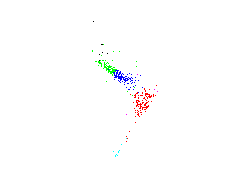
PCA Spectral data NLPCA - Nonlinear PCA - Autoencoder

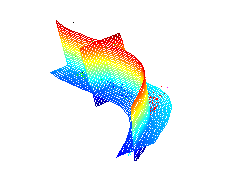
Here, NLPCA is applied to 19-dimensional spectral data representing equivalent widths of 19 absorption lines of 487 stars, available at www.cida.ve. The figure in the middle shows a visualisation of the data by using the first three components of standard PCA. Data of different colors belong to different spectral groups of stars. The first three components of linear PCA and of NLPCA are represented by grids in the left and right figure, respectively. Each grid represents the two-dimensional subspace given by two components while the third one is set to zero. Thus, the grids represent the new coordinate system of the transformation. In contrast to linear PCA (left) which does not describe the nonlinear characteristics of the data, NLPCA gives a nonlinear (curved) description of the data, shown on the right.


Publications by Matthias Scholz

see all publications: [Matthias Scholz: publications]


Related algorithms


See also:

Nonlinear PCA
Matthias Scholz