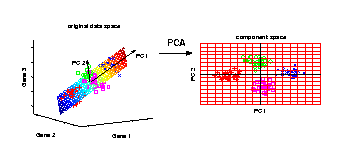
Principal component analysis in Matlab

In Matlab, principal component analysis (PCA) is part of the Statistics Toolbox, see pcacov and princomp. Princomp can be used in the following way:

    data=rand(100,10);  % artificial data set of 100 variables (genes) and 10 samples
    [W, pc] = princomp(data'); pc=pc'; W=W';
    plot(pc(1,:),pc(2,:),'.'); 
    title('{\bf PCA} by princomp'); xlabel('PC 1'); ylabel('PC 2')

But you also can perform PCA by yourself, using eig and cov to calculate the eigenvectors of the covariance matrix:

% consider an artificial data set of 100 variables (e.g., genes) and 10 samples
    data=rand(100,10);

% remove the mean variable-wise (row-wise)
    data=data-repmat(mean(data,2),1,size(data,2));

% calculate eigenvectors (loadings) W, and eigenvalues of the covariance matrix
    [W, EvalueMatrix] = eig(cov(data'));
    Evalues = diag(EvalueMatrix);

% order by largest eigenvalue
    Evalues = Evalues(end:-1:1);
    W = W(:,end:-1:1); W=W';  

% generate PCA component space (PCA scores)
    pc = W * data;

% plot PCA space of the first two PCs: PC1 and PC2
    plot(pc(1,:),pc(2,:),'.')

Note, that this procedure cannot be used when you have extreme high-dimensional data, because of an extreme large variable-times-variable covariance matrix.

How to apply PCA to more than 20.000 variables (genes)?

Classical PCA algorithms are limited when applied to extreme high-dimensional dataset, e.g., to gene expression data in Bioinformatics approaches. But often we only need the first two or three principal components to visualize the data. For extracting only the first k components we can use probabilistic PCA (PPCA) [Verbeek 2002] based on sensible principal components analysis [S. Roweis 1997], e.g, by using this modified PCA matlab script (ppca.m), originally by Jakob Verbeek. It also is applicable to incomplete data sets (missing data).

    data=rand(100,10); % artificial data set of 100 variables (e.g., genes) and 10 samples
    
    [pc,W,data_mean,xr,evals,percentVar] = ppca(data,3);  % download: ppca.m
    
    plot(pc(1,:),pc(2,:),'.');
      title('{\bf PCA}');
      xlabel(['PC 1 (',num2str(round(percentVar(1)*10)/10),'%)',]);
      ylabel(['PC 2 (',num2str(round(percentVar(2)*10)/10),'%)',]);

Update: A new Matlab package by Alexander Ilin includes a collection of several algorithms of PCA to use on high-dimensional data including missing data (Ilin and Raiko, 2010).

GNU R: For probabilistic PCA (PPCA) using GNU R, see the Bioconductor package pcaMethods, also published in Bioinformatics by W. Stacklies et al. (pdf)

Principal component analysis in Matlab

How to apply PCA to more than 20.000 variables (genes)?

See also: